Question

How much more will 22,000 earn in interest than 14000 if both are invested in savings accounts with apys of 5.4% for a year?

Answer 1

$432

Explanation:

Answer 2

$432 more are earned by 22,000 than 14,000 if invested with apys of 5.4% for a year

Explanation:

Total =
`P*(1+r)^t`

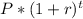
where P=Principal amount

r= rate

t= time

Using this formula for P= 22,000 and r = 5.4% or 0.054 and t= 1

Total =
`22,000*(1+0.054)^1`

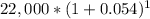
Total =
`23,188`

Interest earned = 23,188 -22,000

Interest earned = 1,188

Using this formula for P= 14,000 and r = 5.4% or 0.054 and t= 1

Total =
`14,000*(1+0.054)^1`

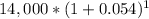
Total =
`14,756`

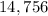
Interest earned = 14,756 -14,000

Interest earned = 756

AS interest earned by 22,000 is 1,188 while interest earned by 14,000 is 756

so, 1,188 - 756 = 432.

So, $432 more are earned by 22,000 than 14,000 if invested with apys of 5.4% for a year