Question

URGENT!! PLEASE HELP!!!

Felix took out an unsubsidized student loan of $40,000 at a 3.6% APR, compounded monthly, to pay for his last six semesters of college. If he will begin paying off the loan in 33 months with monthly payments lasting for 20 years, what will be the amount of his monthly payment?

A. $257.04
B. $258.36
C. $232.85
D. $234.04

Answer 1

The correct option is B.

Explanation:

The formula for amount after compound interest is

`A=P(1+(r)/(n))^(nt)`

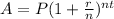
Where P is principal, r is rate of interest, n is number of times interest compounded in a period, t is number of years.

It is given that Felix took out an unsubsidized student loan of $40,000 at a 3.6% APR, compounded monthly. The amount after 33 month is

`A=40000(1+(0.036)/(12))^(33)=44156.1074`

The amount after 33 month is $44156.1074. So, the new principle amount is $44156.1074.

The monthly payment of $44156.1074 for 20 years is

`m=(P.V.(\fracr))/(1-(1+r)^(-n))`

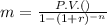
Where, P.V. is present value, r is rate of interest and n is number of times interest compounded.

`m=(44156.1074((0.036)/(12)))/(1-(1+(0.036)/(12))^(-20* 12))`

`m=258.362447711`

`m\approx 258.36`

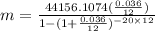
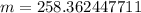
Therefore the correct option is B.