Answer: 109.89 m
Step-by-step explanation:
In order to solve this problem, the figure attached will be helpful.
As we can see, the angle of depression (below the horizontal line) is
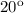 , if we know the angle between the horizontal and the ground (bottom of the cliff) is
, if we know the angle between the horizontal and the ground (bottom of the cliff) is
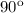 , by simple geometry we will know the other angle is
, by simple geometry we will know the other angle is
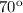 :
:
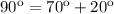
Now, we have a right triangle here and we need to find
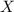 which is istance between buoy and the feet of the cliff, and we can solve this by using the tangent trigonometric function:
which is istance between buoy and the feet of the cliff, and we can solve this by using the tangent trigonometric function:
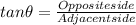 (1)
(1)
Where:
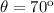
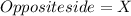
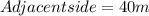
Rewritting equation (1):
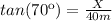 (2)
(2)
Finding
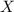 :
:
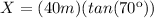 (3)
(3)
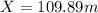 >>>distance between buoy and the cliff
>>>distance between buoy and the cliff