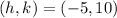Question

Identify the center and radius from the equation of the circle given below. x^2+y^2+121-20y=-10x

Answer 1

Explanation:

x²+y²+121-20y=-10x

(x²+10x)+(y²-20y)+121=0

(x²+10x+25)-25+(y²-20y+100)-100+121=0

(x+5)² + (y-10)²= 2²

the center is : A(-5;10) and radius : r = 2

Answer 2

Center: (-5,10)

Radius: 2

Explanation:

The equation of the circle in center-radius form is:

`(x-h)^2+(y-k)^2=r^2`

Where the point (h,k) is the center of the circle and "r" is the radius.

Subtract 121 from both sides of the equation:

`x^2+y^2+121-20y-121=-10x-121\\x^2+y^2-20y=-10x-121`

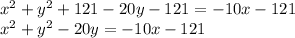
Add 10x to both sides:

`x^2+y^2-20y+10x=-10x-121+10x\\x^2+y^2-20y+10x=-121`

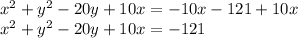
Make two groups for variable "x" and variable "y":

`(x^2+10x)+(y^2-20y)=-121`

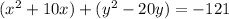
Complete the square:

Add
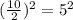`((10)/(2))^2=5^2` inside the parentheses of "x".

Add
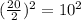`((20)/(2))^2=10^2` inside the parentheses of "y".

Add
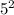`5^2` and
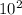`10^2` to the right side of the equation.

Then:

`(x^2+10x+5^2)+(y^2-20y+10^2)=-121+5^2+10^2\\(x^2+10x+5^2)+(y^2-20y+10^2)=4`

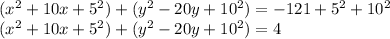
Rewriting, you get that the equation of the circle in center-radius form is:

`(x+5)^2+(y-10)^2=2^2`

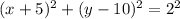
You can observe that the radius of the circle is:

`r=2`

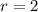
And the center is:

`(h,k)=(-5,10)`