Answer:
The required equation is 7=2+r and the value of r is 5 units.
Explanation:
In the given hanger, the left side of the hanger has 7 boxes in which each box is of one unit.
The sum of left sides is
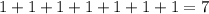
The sum of left side is 7.
Right side of the hanger has 2 boxes in which each box is of one unit and pentagon of r units. So, the sum of right side is
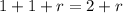
It is given that the hanger represents a balanced equation. It means the left sides is equal to the right side. So, the required equation is

Subtract 2 from both the sides.

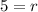
Therefore the required equation is 7=2+r and the value of r is 5 units.