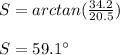Question

If r=20.5 and s=34.2 find S Round to the nearest tenth

Answer 1

59.1 °

Explanation:

tan S = 34.2 / 20.5

S = tan -1 (34.2 / 20.5)

S = 59.1 ° Rounded to the nearest tenth!

Answer 2

Answer: option d

Explanation:

Remember the identity:

`tan\alpha=(opposite)/(adjacent)`

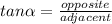
The inverse of the tangent function is arctangent. You need to use this to calculate the angle "S":

`\alpha =arctan((opposite)/(adjacent))`

Knowing that: you need to find the measure of the angle "S" ,
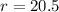`r=20.5` (which is the adjacent side) and
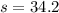`s=34.2` (which is the opposite side), you can sustitute values into
`\alpha =arctan((opposite)/(adjacent))`

Then, you get that the measure of "S" rounded to the nearest tenth is:

`S=arctan((34.2)/(20.5))\\\\S=59.1\°`