Answer:
There are two unique triangles that can be formed two side lengths of 10 centimeters and one 40º angle.
Explanation:
There are theoretically three unique triangles that can be formed with two side lengths of 10 centimeters and one 40º angle. We include a representation of possible triangles:
Case A - Law of Cosine (
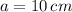 ,
,
 ,
,
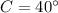 )
)
 (1)
(1)
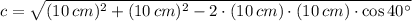
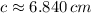
Case B - Laws of Sine and Cosine (
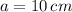 ,
,
 ,
,
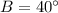 )
)
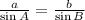 (2)
(2)
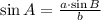
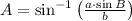
![A = \sin^(-1)\left[((10\,cm)\cdot (\sin 40^(\circ)))/(10\,cm) \right]](https://img.qammunity.org/2022/formulas/mathematics/high-school/s99oxlm4qz2uf78ck48bth221c7avg4bmf.png)

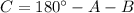
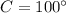

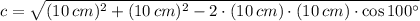
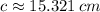
Case C - Laws of Sine and Cosine (
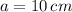 ,
,
 ,
,
 )
)
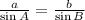
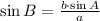
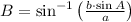
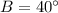
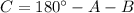
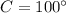

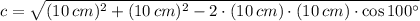
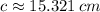
There are two unique triangles that can be formed two side lengths of 10 centimeters and one 40º angle.