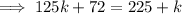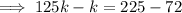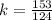The polynomial ky^3+3y^2-3 and 2y^3-5y+k when divided by (y-5) leave the same remainder in each case. Find the value of k.

Question

asked Mar 26, 2020 212k views

1 Answer

Alireza Eliaderani · Answer 1 · 2020-03-31T08:10:37+0000

Answer:

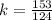
k=(153)/(124)

Explanation:

According to the Remainder Theorem; when P(y) is divided by y-a, the remainder is p(a).

The first polynomial is :

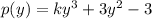
p(y)=ky^3+3y^2-3

When p(y) is divided by y-5, the remainder is

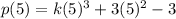
p(5)=k(5)^3+3(5)^2-3

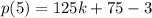
p(5)=125k+75-3

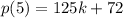
p(5)=125k+72

When the second polynomial:

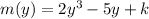m(y)= 2y^3-5y+k is divided by y-5.

The remainder is;

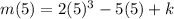
m(5)= 2(5)^3-5(5)+k

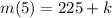
m(5)= 225+k

The two remainders are equal;

$\implies 125k+72=225+k$

$\implies 125k-k=225-72$

$\implies 124k=153$

k=(153)/(124)