Question

Rewrite the function by completing the square. f(x)=x^2+x-30 It’s supposed to look like this f(x)= (x+ )^2+ .

Answer 1

`f(x)=(x+1/2)^2 +(- 30.25)`

Explanation:

In this question we are required to rewrite the given function by using completing the square method.

Completing the square method requires that our given equation can be written in form:
`(a\pm b)^2 = a^2 \pm 2ab +b^2`

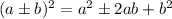
SO, we have to transform our equation according to above format.

Since our equation is
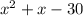`x^2+x-30`, we will transform it into

`(a + b)^2 = a^2 + 2ab +b^2`

because the middle term of given equation has + sign.

`x^2+x-30=0\\x^2+x=30\\x^2 + 2(x)(1/2) + (1/2) ^2 = 30 + (1/2)^2`

We have introduced (1/2)^2 on both sides of the equation to gain the required form.

`(x+1/2)^2 = 30.25\\(x+1/2)^2 - 30.25 = 0\\f(x) = (x+1/2)^2 +(- 30.25)`

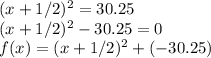
Our answer is
`f(x)=(x+1/2)^2 +(- 30.25)`