Question

Simplify the following polynomial expression

(3x^2-x-7)-(5x^2-4x-2)+(x+3)(x+2)

Answer 1

The polynomial simplifies to an expression that is a - x^2+8x+1 with a degree of 2.

Explanation:

(3x^2-x-7)-(5x^2-4x-2)+(x+3)(x+2)

By MDAS, we will start with multiplication using the foil method

(3x^2-x-7)-(5x^2-4x-2)+(x^2+2x+3x+6)

Combine like terms in each parenthesis

(3x^2-x-7)-(5x^2-4x-2)+(x^2+5x+6)

Distribute the negative sign

3x^2- x- 7- 5x^2+ 4x + 2+x^2 + 5x +6, combine like terms

4x^2-5x^2+8x+1

-x^2+8x+1.

Answer 2

Hello!

The answer is:

The simplified form of the given polynomial is:

`-x^(2)+8x+1`

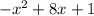
Why?

In order to simplify de given polynomial, we need to group the the like terms.

Remember, like the terms are terms that share the same variable and the same exponent.

For example:

`x^(2) +2x^(2) +3x^(3) +2=3x^(2) +3x^(3) +2`

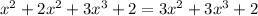
We only operate with the variables that shares the same exponent.

Also, we need to remember the distributive property:

`(a+b)(c+d)=ac+ad+bc+bd`

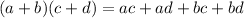
So, we are given the polynomial:

`(3x^(2)-x-7)-(5x^(2)-4x-2)+(x+3)(x+2)`

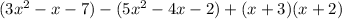
Simplifying we have:

`(3x^(2)-x-7)-(5x^(2)-4x-2)+(x+3)(x+2)=3x^(2)-x-7-5x^(2)+4x+2+((x*x)+(2*x)+(3*x)+(3*2))\\\\(3x^(2)-x-7)-(5x^(2)-4x-2)+(x+3)(x+2)=-2x^(2)+3x-5+(x^(2)+2x+3x+6)\\\\(3x^(2)-x-7)-(5x^(2)-4x-2)+(x+3)(x+2)=-x^(2)+8x+1`

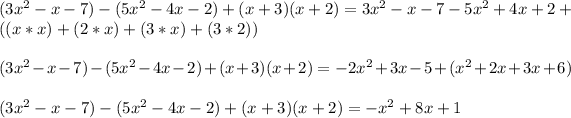
Hence, the simplified form of the given polynomial is:

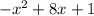`-x^(2)+8x+1` and it's a polynomial with a degree of 2.

Have a nice day!