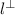Question

(1 pt) let l be the line given by the span of \left[\begin{array}{c} 2\cr -6\cr 9 \end{array}\right] in \mathbb{r}^3. find a basis for the orthogonal complement l^{\bot} of l.

Answer 1

Two vectors are orthogonal if their scalar product is zero. Also, since we have a subspace of dimension 1 (the line) in a space of dimension 3 (R^3), the orthogonal complement has dimension 2.

This means that we're looking for a basis of the 2-dimensional subspace of R^3 defined by the property

`l^(\bot) = \left\{(x,y,z) \in \mathbb{R}^3\ :\ (2, -6, 9)\cdot (x,y,z) = 0\right\}`

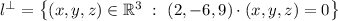
By definition, this means we want

`2x-6y+9z=0`

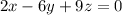
and we can deduce

`2x-6y+9z=0 \iff z = (-2x+6y)/(9)`

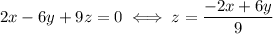
We obviously have 2 degree of freedom here (we're building a base of a 2-dimensional space): we can write a generic vector of
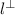`l^(\bot)` as

`\left(x, y, (-2x+6y)/(9)\right) = \left(x, 0, (-2x)/(9)\right) + \left(0, y, (6y)/(9)\right) = x\left(1,0,(2)/(9)\right) + y\left(0, 1, (2)/(3)\right)`

In other words, we just proved that any vector of
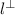`l^(\bot)` can be written as a certain linear combination of vectors (1,0,-2/9) and (0,1,2/3), which means that they are a base of
`l^(\bot)`