Answer:
a) T(3,0)
b) |CT|=2.83
c) |DT|=4.47
Explanation:
The given parallelogram CARD has vertices (5, -2), (-1, -2), (1, 2), and (7, 2)
The diagonals of a parallelogram bisect each other.
Find the midpoint of one diagonal, that gives us the point of intersection of the diagonals T.
The midpoint of C(5,-2) and (1,2) is
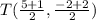

b) To find the length of CT, we use the distance formula; where C(5,-2) ahd T(3,0).


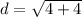
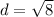

The length of CT is 2.83 to the nearest hundredth
c) To find the length of DT, we use the distance formula; where D(7,2) ahd T(3,0).

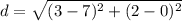
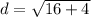
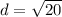
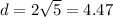
The length of DT is 4.47 to the nearest hundredth