Question

9 min left please help

Answer 1

the answer for this question is 20 x cube by 5

Answer 2

For this case, we must simplify the following expression:

`\sqrt [3] {\frac {4x} {5}}`

For this, we follow the steps below:

We rewrite the expression as:

`\frac {\sqrt [3] {4x}} {\sqrt [3] {5}}`

We multiply by:

`\frac {(\sqrt [3] {5}) ^ 2} {(\sqrt [3] {5}) ^ 2}\\\frac {\sqrt [3] {4x}} {\sqrt [3] {5}} * \frac {(\sqrt [3] {5}) ^ 2} {(\sqrt [3] {5}) ^ 2} =`

We have by definition of multiplication of powers of equal base that:

`a ^ m * a ^ n = a ^ {m + n}`

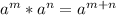
So:

`\\\frac {\sqrt [3] {4x} * (\sqrt [3] {5}) ^ 2} {\sqrt [3] {5}) ^ 3} =\\\frac {\sqrt [3] {4x} * (\sqrt [3] {5}) ^ 2} {5} =`

We know that:

`(\sqrt [3] {5}) ^ 2 = \sqrt [3] {5 ^ 2}`

So, we have:

`\frac {\sqrt [3] {4x} * \sqrt [3] {5 ^ 2}} {5} =\\\frac {\sqrt [3] {4x} * \sqrt [3] {25}} {5} =\\\frac {\sqrt [3] {100x}} {5}`

Answer:

Option c