Question

Write a rule to describe the function shown. x y −6 −4 −3 −2 0 0 3 2 y equals start fraction two over three end fraction x y equals negative start fraction two over three end fraction x y equals start fraction three over two end fraction x y equals start fraction two over three end fraction x minus one

Answer 1

to make it short its A

Explanation:

Answer 2

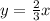`y=(2)/(3) x` (y equals start fraction two over three end fraction x)

Explanation:

Lest's organize the table values of our function first:

x y

-6 -4

-3 -2

0 0

3 2

The simplest kind of of function is a linear function of the form
`y=mx+b` where
`m` is the slope and
`b` is the y-intercept. Let's us check if our function is a linear one finding its equation and checking that all points are in the line.

The first step to find a linear equation is find the slope of the line; to do it, we are using the slope formula:

`m=(y_2-y_1)/(x_2-x_1)`

where

`m` is the slope of the line

`(x_1,y_1)` are the coordinates of the first point

`(x_2,y_2)` are the coordinates of the second point

We know from our table that the first and second points are (-6, -4) and (-3, -2) respectively, so
`x_1=-6`,
`y_1=-4`,
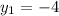`x_2=-3`, and
`y_2=-2`.

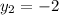Replacing values:

`m=(y_2-y_1)/(x_2-x_1)`

`m=(-2-(-4))/(-3-(-6))`

`m=(-2+4)/(-3+6))`

`m=(2)/(3))`

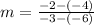
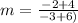
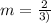
Now that we have the slope of our line we can use the point slope formula to complete our linear function:

`y-y_1=m(x-x_1)`

where

`m` is the slope

`(x_1,y_1)` are the coordinates of the first point

Replacing values:

`y-y_1=m(x-x_1)`

`y-(-4)=(2)/(3))(x-(-6))`

`y+4=(2)/(3))(x+6)`

`y+4=(2)/(3) x+4`

`y=(2)/(3) x+4-4`

`y=(2)/(3) x`

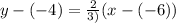
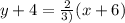
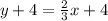
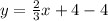
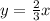
Now, to check if our function is valid, we can either check if each point satisfies the rule
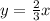`y=(2)/(3) x`, or we can graph it and check if each lies is in the graph.

Let's check both:

We already know that points (-6, -4) and (-3, -2) satisfy the rule (after all, those were the point we used to came out with the rule in the first place), so we just need to check the points (0, 0) and (3, 2)

- For (0, 0):

`y=(2)/(3) x`

`0=(2)/(3)(0)`

`0=0`

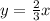
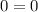
The point satisfies the rule.

- For (3, 2):

`y=(2)/(3) x`

`2=(2)/(3) (3)`

`2=2`

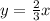
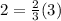
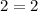
The point satisfies the rule.

Since all the points of our table satisfies the rule
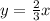`y=(2)/(3) x`, we can conclude that the rule describing the function shown is
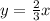`y=(2)/(3) x`.