Answer:
He invested $125,000 at 6% and $423,000 at 7%.
Explanation:
Let
 be the amount of money invested at 6%. Since the amount of money invested at 7% is 3 times the amount of money invested at 6% plus $48,000,
be the amount of money invested at 6%. Since the amount of money invested at 7% is 3 times the amount of money invested at 6% plus $48,000,
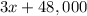 is the amount invested at 7%.
is the amount invested at 7%.
We know that both investments yield $37,110 in interest, so the sum of the money invested at 6% and the money invested at 7% is $37,110; in other words:
6%
 +7%
+7%
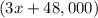 = 37,110
= 37,110
We need to convert both interest rates to decimals, so we are going to divide both rates by 100%
6%
 +7%
+7%
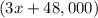 = 37,110
= 37,110


Now we can solve our equation, step-by-step, to find the amount of each investment.
Step 1. Distribute 0.07 to 3x and 48,000

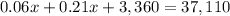
Step 2. Combine like terms
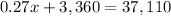
Step 3. Subtract 3,360 from both sides of the equation
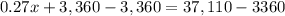
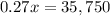
Step 4. Divide both sides of the equation by 0.27
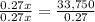
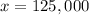
We now know that he invested $125,000 at 6%. Since the amount invested at 7% is
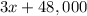 , we just need to replace x with 125,000 to find it:
, we just need to replace x with 125,000 to find it:
Amount invested at 7% =
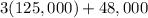
Amount invested at 7% =
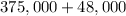
Amount invested at 7% =
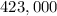
We can conclude that the actor invested $125,000 at 6% and $423,000 at 7%.