Question

A parabola with a vertex at (0,0) has a directrix that crosses the negative part of the y-axis.

Which could be the equation of the parabola?

Answer 1

The actually answer is x(2) = 4y

Answer 2

`\boxed{x^2=4py}`

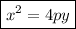
Explanation:

A parabola is the set of all points that lies on a plane and are equidistant from a fixed line called the directrix and a fixed point called focus, that doesn't lies on the line. If the vertex is at the origin and the directrix crosses the negative part of the y-axis, then the equation takes the following forms:

`\boxed{x^2=4py}`

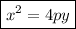
Where the focus lies on the axis
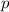`p \units` (directed distance) from the vertex.

The representation of this problem is shown below. As you can see, the vertex lies on the origin while the directrix crosses the negative part of the y-axis.