Question

Given: 3x - 2 ≤ 2x + 1.

Choose the solution set.
x R, x ≤ 1
x R, x ≤ 3
x R, x ≤ -3
x

Answer 1

second option is correct:)

Explanation:

Answer 2

`\boxed{\boxed{\pink{\bf \leadsto Option \ second\ is \ correct . }}}`

Explanation:

A linear inequality is given to us . And we need to find the correct number line. So the given linear inequality is :-

`\bf\implies 3x -2 \leq 2x + 1 \\\\\bf\implies 3x -2x \leq 2 + 1 \\\\\bf\implies x \leq 2 + 1 \\\\\bf\implies\boxed{\red{\bf x \leq 3 }}`

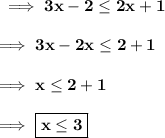
This means that the value of x can be less than or equal to 3 . That is it means x ≤ 3. So , the required solution set will be ,

`\boxed{\purple{\bf \{x | x \in \mathbb{R} , x \leq 3 \}}}`

Hence the second option is correct.