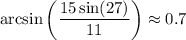As suggested, we have to use the law of sines: it states that the ratio between a side and the sine of the opposite angle is constant in every triangle.
We know that one side length is 11, and the opposite angle is 27°
Another side length is 15, and the opposite angle is x.
So, the law of sines states that
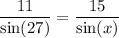
Solving for
 we have
we have
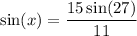
Which implies
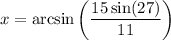
Put this into a calculator to get