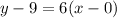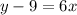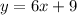Question

A given line has the equation 2x + 12y = −1. What is the equation, in slope-intercept form, of the line that is perpendicular to the given line and passes through the point (0, 9)?

Answer 1

y = 6x + 9

Explanation:

The equation of a line in slope- interceot form is

y = mx + c ( m is the slope and c the y- intercept )

Rearrange 2x + 12y = - 1 into this form

Subtract 2x from both sides

12y = - 2x - 1 ( divide all terms by 12 )

y = -
`(1)/(6)` x -
`(1)/(12)` ← in slope- intercept form

with slope m = -
`(1)/(6)`

Given a line with slope m then the slope of a line perpendicular to it is

`m_(perpendicular)` = -
`(1)/(m)` = -
`(1)/(-(1)/(6) )` = 6

Note the line passes through (0, 9) on the y- axis ⇒ c = 9

y = 6x + 9 ← equation of perpendicular line

Answer 2

`y=6x+9`

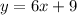
Explanation:

Given equation of the line,

`2x + 12y = -1`

`12y=-2x-1`

`y=-(1)/(6)x-(1)/(12)`

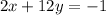
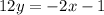
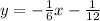
Slope intercept form of a line is y = mx + c,

Where, m is the slope of the line,

By comparing, the slope of the given line is
`(-1)/(6)`,

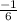Since, when two lines are perpendicular then the product of their slope is -1,

Let
`m_1` be the slope of the perpendicular line of the given line,

`m_1* -(1)/(6)=-1`

`\implies m_1=6`

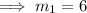
Now, point slope intercept form of a line is,

`y_y_1=m(x-x_1)`

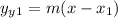
Where,
`(x_1, y_1)` is the point on the line,

Hence, the equation of the line passes through the point (0, 9) and having slope 6 is,

`y-9=6(x-0)`

`y-9=6x`

`y=6x+9`