Answers:
In convex mirrors the focus is virtual and the focal distance is negative. This is how the reflected rays diverge and only their extensions are cut at a point on the main axis, resulting in a virtual image of the real object .
a) Position of the soda bottle (the object)
The Mirror equation is:
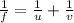(1)
Where:
is the focal distance
is the distance between the object and the mirror
is the distance between the image and the mirror
We already know the values of
and
, let's find
from (1):
(2)
Taking into account the explanation at the beginign of this asnswer:
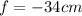and
The negative signs indicate the focal distance and the distance between the image and the mirror are virtual
Then:
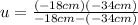
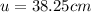(3) >>>>Position of the soda bottle
b) magnification of the image
The magnification
of the image is given by:
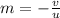(4)
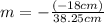
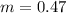(5)>>>the image is 0.47 smaller than the object
The fact that this value is positive means the image is upright
c) Describe the image
According to the explanations and results obtained in the prior answers, the correct option is 9:
The image is virtual, upright, smaller than the object
d) Height of the soda bottle (object)
Another way to find the magnification is by the following formula:
(6)
Where:
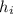is the image height
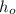is the object height
We already know the values of
and
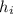, let's find
:
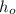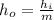(7)
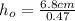
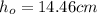(8) >>>height of thesoda bottle