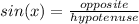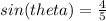Question

If cos theta = -3/5 in quadrant 2, what is sin theta?

Answer 1

hello : sin(θ) = 4/25

Explanation:

you know : cos²(θ) + sin²(θ) =1 and : cos(θ) = - 3/5

(-3/5)² + sin²(θ) =1

9/25 + sin²(θ) =1

sin²(θ) =1 -9/25

sin²(θ) = 16/25

sin(θ) = 4/25 or sin(θ) = - 4/25

in quadrant 2 : sin(θ) > 0

so : sin(θ) = 4/25

Answer 2

`sin(theta)=(4)/(5)`

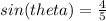
Explanation:

if cos theta = -3/5 in quadrant 2, find out sin(theta)

`cos(x)=(-3)/(5)`

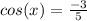
cos is negative in second and third quadrant

Here cos is in second quadrant.

Sin is positive in second quadrant .

`cos(x)=(adjacent)/(hypotenuse)`

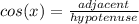
adjacent side= 3 , hypotenuse = 5

Lets use Pythagorean theorem
`c^2=a^2 + b^2`

`5^2=3^2 + b^2`

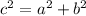
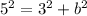
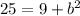`25=9 + b^2` Subtract 9 from both sides

`b^2= 16`

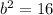
b=4

opposite side = 4

`sin(x)=(opposite)/(hypotenuse)`

`sin(theta)=(4)/(5)`