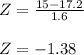Answer:
Z-score = -1.38
Explanation:
The z-score measures how many standard deviations from the mean a data is
Therefore the z score is the quotient between the difference between a value and the mean and the standard deviation
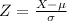
Where
μ is the mean, x is a data of the population and
 is the standard deviation
is the standard deviation
In this case
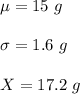
Then the z-score is