Answer:
the required equation is:

Explanation:
The equation given is:
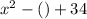
Comparing it with standard quadratic equation
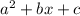
a= 1,
b=?
C= 34
We can find the value of b using Vieta's formulas :
That states that if roots x₁ and x₂ are given then,
x₁ + x₂ = -b/a
We are given roots: 5 ± 3i i.e, x₁= 5 + 3i and x₂= 5 - 3i
solving
5 + 3i + 5 - 3i = -b/1
10 = -b
Since the given equation already gives b as -b so, -b= 10 => b=10
Putting value of b in the missing place the required equation will be:
