Answer:
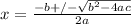
Explanation:
The standard form of a quadratic equation in x can be written as;

where a,b, and c are constants.
The first step is to subtract c on both sides of the equation;

The next step is to divide both sides of the equation by the constant a;
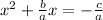
Next, we complete the square on the left hand side of the equation by determining another constant c as;
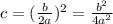
We then add this constant on both sides of the equation in order to complete the square on the L.H.S;
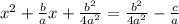
The expression on the L.H.S of the equation is now a perfect square and can be factorized to yield;
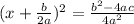
We then take square roots on both sides of the equation and simplify the expression on the R.H.S;
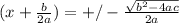
The final step is to make x the subject of the formula and a little simplification which will yield the quadratic formula;
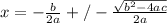
Putting the expression on the R.H.S under a common denominator yields;
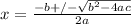
which is the quadratic formula