Answer:
The length of b is 6.7
Explanation:
You have way too many unknowns to do much of anything with this. The only way out is to use one of the three geometric means formulas for right triangles. The one that applies here is
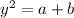
and since a + b = 15,
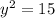
and

Now we look to the right triangle that contains the base b. It has a given angle of 30 degrees, and now we know the side length across from the 30 degrees, we have to think of the trig ratio that relates an angle to the side opposite that angle and to the side adjacent to that angle. That's the tangent ratio. As follows:

and solving for b:
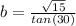
Do this in degree mode in your calculator and you'll get that b = 6.7