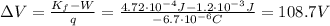Question

The work done by an external force to move a -6.70 μc charge from point a to point b is 1.20×10−3 j .

part a



if the charge was started from rest and had 4.72×10−4 j of kinetic energy when it reached point b, what must be the potential difference between a and b?

Answer 1

108.66V

Step-by-step explanation:

E = 1.20*10⁻³J

q = 6.70μC = 6.7*10⁻⁶C

V =?

K.E = 4.72 * 10⁻⁴J

E = q∇v

but there's difference in energy in moving the electron from point A to B. The electron has an initial energy of 4.72*10⁻⁴J.

E = Q - KE

E = 1.20*10⁻³ - 4.72*10⁻⁴ = 7.28*10⁻⁴J

E = q∇v

∇v = E / q

∇v = 7.28*10⁻⁴ / 6.7*10⁻⁶

∇v = 108.66V

the change in potential difference from point A to B was 108.66V

Answer 2

108.7 V

Step-by-step explanation:

Two forces are acting on the particle:

- The external force, whose work is
`W=1.20 \cdot 10^(-3)J`

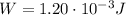
- The force of the electric field, whose work is equal to the change in electric potential energy of the charge:
`W_e=q\Delta V`

where

q is the charge

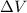`\Delta V` is the potential difference

The variation of kinetic energy of the charge is equal to the sum of the work done by the two forces:

`K_f - K_i = W + W_e = W+q\Delta V`

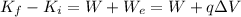
and since the charge starts from rest,
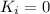`K_i = 0`, so the formula becomes

`K_f = W+q\Delta V`

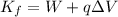
In this problem, we have

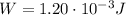`W=1.20 \cdot 10^(-3)J` is the work done by the external force

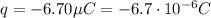`q=-6.70 \mu C=-6.7\cdot 10^(-6)C` is the charge

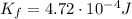`K_f = 4.72\cdot 10^(-4)J` is the final kinetic energy

Solving the formula for
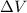`\Delta V`, we find

`\Delta V=(K_f-W)/(q)=(4.72\cdot 10^(-4)J-1.2\cdot 10^(-3) J)/(-6.7\cdot 10^(-6)C)=108.7 V`