Answer:
correct option for first blank is 5/4 and for second blank is
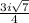
i.e m=
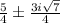
Explanation:
The given equation
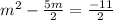
and we have to find m= ______ ± ________
We can use quadratic formula to solve this question.
The above equation can be written as:
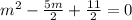
and the formula used will be:

Putting values of a= 1, b= -5/2 and c= 11/2 and solving we get:
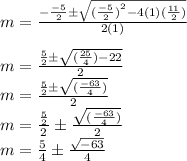
Since there is - sign inside the √ so
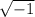 is equal to i and we have to divide
is equal to i and we have to divide
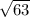 into its multiples such that the square root of one multiple is whole no so,
into its multiples such that the square root of one multiple is whole no so,
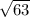 =
=
 =
=
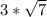
Putting value of
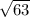 and
and
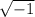
the value of m=
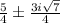
so, correct option for first blank is 5/4 and for second blank is
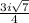 .
.