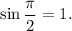Answer:
D
Explanation:
1. Remind that

Here you can use trigonometric table to find the value of
 , or you can remind that
, or you can remind that
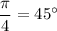 and
and
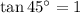 because special right triangle 45°-45°-90° is isosceles (with congruent oppposite and adjacent legs) and the ratio between the opposite leg and adjacent leg is equal to 1.
because special right triangle 45°-45°-90° is isosceles (with congruent oppposite and adjacent legs) and the ratio between the opposite leg and adjacent leg is equal to 1.
2. Now
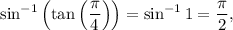
because