Question

What is the domain and range of this function?

F(x) = log ˯5(x-2) +1

A. Domain: x> -2; range; all positive real numbers.

B. Domain: x>2; range: all positive real numbers

C. Domain: x>-2; range: all real numbers

D. Domain; x>2; range: all real numbers

Answer 1

As for the domain, the only restriction comes from the logarithm. The argument of a logarith must be strictly positive, so we have

`x-2>0 \iff x>2`

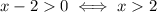
As for the range, we have:

• The range of
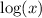  `\log(x)` are all real numbers
• If we change to
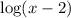  `\log(x-2)` we're translating the function horizontally, so the range remains the same
• If we change to
  `\log(5(x-2()` we're stretching the function horizontally, so the range doesn't change
• If we change to
  `\log(5(x-2))+1` we're translating the function 1 unit up, but the range is already all the real numbers, so it doesn't change.