Answer:
See explanation
Explanation:
Zeroe of the function is such velue of x at which f(x)=0.
1. Consider the function
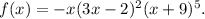
Zeros are:
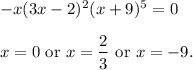
Zero
 has multiplicity of 1, zero
has multiplicity of 1, zero
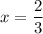 has multiplicity of 2, zero
has multiplicity of 2, zero
 has multiplicity of 5.
has multiplicity of 5.
At
 or
or
 the graph of the function crosses the x-axis, at
the graph of the function crosses the x-axis, at
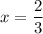 the graph of the function touches the x-axis.
the graph of the function touches the x-axis.
2. Consider the function
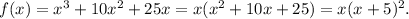
Zeros are:
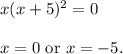
Zero
 has multiplicity of 1, zero
has multiplicity of 1, zero
 has multiplicity of 2.
has multiplicity of 2.
At
 the graph of the function crosses the x-axis, at
the graph of the function crosses the x-axis, at
 the graph of the function touches the x-axis.
the graph of the function touches the x-axis.