Answer:
A. 12.4
Explanation:
To find a, we'll use the Law of Sines that says:

And we'll isolate a to get:
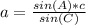
We first need to find A, which is easy. The sum of the interior angles of a triangle is 180 degrees... and we already have 2 of them, so:
A = 180 - 90 - 16.75 = 73.25
(converted 16°45' to 16.75)
Then we will plug-in the information we already have

So, let's round it to 12.4 to match the answer A.