Question

Based on the graph, which statement BEST describes the acceleration of the two objects?

A) Acceleration 1 - no acceleration. Acceleration 2 - negative acceleration.
B) Acceleration 1 - no acceleration. Acceleration 2 - speeds up and slows down.
C) Acceleration 1 - constant acceleration. Acceleration 2 - varied acceleration.
D) Acceleration 1 - positive acceleration. Acceleration 2 - negative acceleration.

Answer 1

Answer:C) Acceleration 1 - constant acceleration. Acceleration 2 - varied acceleration.

Step-by-step explanation:

The lines on the graph are best described by the following: Acceleration 1 - constant acceleration. Acceleration 2 - varied acceleration. Acceleration 1 DOES show positive acceleration, but since the slope of the line does not vary, the acceleration is constant. Acceleration B has a varied slope, and therefore, a varied acceleration. It does happen to be positive and negative. For zero acceleration, the slope slope would be zero and the line horizontal.

Answer 2

C) Acceleration 1 - constant acceleration. Acceleration 2 - varied acceleration.

Step-by-step explanation:

In a velocity-time graph, the acceleration corresponds to the slope of the curve.

In fact, acceleration is defined as the ratio between the change in velocity and the time interval:

`a=(\Delta v)/(\Delta t)`

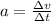
However, we see that in a velocity-time graph,
`\Delta v` corresponds to the increment in the y-variable (
`\Delta y`), while
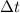`\Delta t` corresponds to the increment in the x-variable (
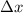`\Delta x`). Therefore, acceleration can also be written as

`a=(\Delta y)/(\Delta x)`

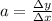
which is exactly the definition of slope of the curve.

Now we notice that:

- For object 1, the slope is constant: this means that the acceleration is constant

- For object 2, the slope varies: this means that the acceleration varies as well