Part 1)
Let's analyze each part of the function:
FROM x = 0 TO x = 5:
We can find the equation of this line by using The Slope-Intercept Form of the Equation of a Line, that states:
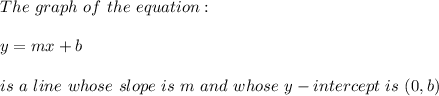
So the y-intercept here is
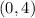 and
and
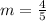 , therefore:
, therefore:
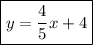
FROM x = 0 TO x = 5:
From the previous line, we know that at
 the output is:
the output is:
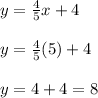
So the point
 lies on both lines.
lies on both lines.
For this new line, the slope is
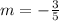
So, with the Point-Slope Form of the Equation of a Line we can find the equation of this other line:
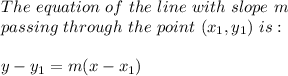
So:
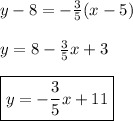
The graph is shown below.
Part 2)
The graph of the linear function
 is a line with slope
is a line with slope
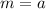 and
and
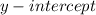 at
at
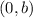 . From the items, we can assure that the following equations are linear functions:
. From the items, we can assure that the following equations are linear functions:

In conclusion, the other functions are nonlinear and they are:
