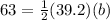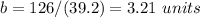Question

If the length of a leg of a triangle is 39.2 and the area of the triangle is 63 what is the length of the other leg

Answer 1

The length of the other leg is
`3.21\ units`

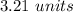
Explanation:

I will assume that the triangle is a right triangle

In a right triangle the legs are perpendicular

so

The area of a right triangle is equal to

`A=(1)/(2)(a)(b)`

where

a and b are the legs of the triangle

In this problem we have

`a=39.2\ units`

`A=63\ units^(2)`

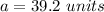
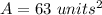
substitute the values

`63=(1)/(2)(39.2)(b)`

`126=(39.2)(b)`

`b=126/(39.2)=3.21\ units`