Answer:
The answer is expression 4㏒w(x² - 6) - (1/3)㏒w(x² + 8) ⇒ 3rd answer
Explanation:
* Lets revise some rules of the logarithmic functions
- log(a^n) = n log(a)
- log(a) + log(b) = log(ab) ⇒ vice versa
- log(a) - log(b) = log(a/b) ⇒ vice versa
* Lets solve the problem
- The expression is
![log_(w)\frac{(x^(2)-6)^(4)}{\sqrt[3]{x^(2)+8}}](https://img.qammunity.org/2020/formulas/mathematics/college/ylsynp2aqeyn40hvbhq1d43v3jj4ftrn1d.png)
∵ log(a/b) = log(a) - log(b)
∴
![log_(w)(x^(2)-6)^(4)-log_(w)\sqrt[3]{x^(2)+8}](https://img.qammunity.org/2020/formulas/mathematics/college/ultejg3hgoaimuahqk3numopqcrlbgyr3s.png)
∵ ∛(x² + 8) can be written as (x² + 8)^(1/3)
∵ log(a^n) = n log(a)
∴
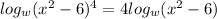
∴
![log_(w)\sqrt[3]{x^(2)+8}=(1)/(3) log_(w) (x^(2)+8)](https://img.qammunity.org/2020/formulas/mathematics/college/f94hatceszqsxy2evgbqy1w183pcue4y60.png)
∴

* The answer is expression 4㏒w(x² - 6) - (1/3)㏒w(x² + 8)