Answer:
a) (5, 11)
b) r = 9
c) (-4, 11)
Explanation:
The equation of a circle in standard form:

(h, k) - center
r - radius
We have the equation:
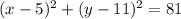
Therefore
a) h = 5, k = 11 → the center (5, 11)
b) r² = 81 → r = √81 = 9 - radius
c) We choose any value of x, but one which h - r ≤ x ≤ h + r
5 - 9 = -4
5 + 9 = 14
-4 ≤ x ≤ 14
Let x = -4. Put to the equation and solve for y:
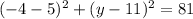
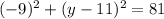
 subtract 81 from both sides
subtract 81 from both sides
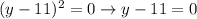 add 11 to both sides
add 11 to both sides
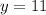
(-4, 11)