Question

Suppose you take a trip to a distant universe and find that the periodic table there is derived from an arrangement of quantum numbers different from the one on Earth. The rules in that universe are: principal quantum number ????=1,2,... (as on Earth); angular momentum quantum number ℓ=0,1,2,...,????−1 (as on Earth); magnetic quantum number ????ℓ=0,1,2,...,ℓ (only positive integers up to and including ℓ are allowed); spin quantum number ????s=−1,0,+1 (that is, three allowed values of spin). Assuming that the Pauli exclusion principle remains valid in the distant universe, what is the maximum number of electrons that can populate a given orbital there? maximum number electrons per orbital: Write the electronic configuration of the element with atomic number 8 in the periodic table. Superscript numbers where appropriate but omit parentheses. electronic configuration:

Answer 1

Part a

The maximum number of electrons that can populate a given orbital are 3.

Part b

Electronic configuration of the element with atomic number 8 is
`1s^3, 2s^3, 2p^2`

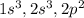
Part c

The atomic number of the second noble gas is 12.

Part a

Since on Earth, the Pauli’s exclusion principle is followed, hence the spin quantum number has two values + 1/2 and − 1/2 and only 2 electrons of opposite spin can occupy one orbital. If the number spin quantum number has 3 values: -1, 0 and +1, then it will have 3 electrons of each spin in each orbital.

From the statement of Pauli’s exclusion principle, it can be found that now 3 electrons will be present in 1 orbital.

The maximum number of electrons that can populate a given orbital are 3.

part b

Each orbital can occupy 3 electrons. Then s orbital also occupies 3 electrons then electronic configuration of the element with atomic number 8 becomes
`1s^3, 2s^3, 2p^2`

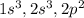
The principle quantum number and the azimuthal quantum number have same values as on Earth, their values will be same. Since the spin quantum number has 3 values, it can now accommodate 3 electrons in each orbital.

Electronic configuration of the element with atomic number 8 is
`1s^3, 2s^3, 2p^2`

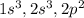
For an element to behave as a noble gas it should have a completely filled orbital. Therefore, the first noble gas will have the configuration
`1s^3`

The second noble gas will have a completely filled 1s, 2s and 2p orbital and p orbital will have two subshells because for l = 1
`m_1` will be 0 and 1. So, its configuration is
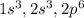`1s^3, 2s^3, 2p^6`and its atomic number is 12.

The principle quantum number and the azimuthal quantum number have same values as on Earth, their values will be same. Since the spin quantum number has 3 values, it can now accommodate 3 electrons in each orbital. Hence, there will be 3 electrons present in both 1s and 2s orbitals. Now for 2p orbitals, the magnetic quantum number will be positive and have 2 values 0 and 1. Hence it will be able to accommodate 6 electrons i.e. 3 electrons in subshell with magnetic quantum number 0 and 3 electrons in subshell with magnetic quantum number 1.

Question:-

Suppose you take a trip to a distant universe and find that the periodic table there is derived from an arrangement of quantum numbers different from the one on Earth. The rules in that universe are:

1. principal quantum number n = 1, 2, . . . (as on Earth);

2. angular momentum quantum number l = 0, 1, 2,. . . , n – 1 (as on Earth);

3. magnetic quantum number ml = 0, 1, 2, . . . , l (only positive integers up to and including l are allowed);

4. spin quantum number ms = –1, 0, 1 (that is, three allowed values of spin).

(a) Assuming that the Pauli exclusion principle remains valid, what is the maximum number of electrons that can populate a given orbital?

(b) Write the electronic configuration of the element with atomic number 8 in the periodic table.

(c) What is the atomic number of the second noble gas?

Answer 2

• Maximun number of electrons per orbital: 3
• Electron configuration of the element with atomic number 8:

1s³ 2s³ 2p²

Step-by-step explanation:

1) Pauli's exclusion principle.

Pauli's exclusion principle states that none two electrons of an atom may have the same set of quantum numbers.

Since the real rule (in our normal universe) is that the spin quantum number can only have two values (s = +1/2 or -1/2), that implies that only two electrons can populate a given orbital here.

2) Rules in the distant universe.

• The rules for the principal quantum number (n), and the angular momentum quantum number (ℓ), are the same of the Earth.

• The rule for the magnetic quantum number (mℓ) is different than in the Earth:

- In the Earth: mℓ = from - ℓ to + ℓ

- In the distant universe: mℓ = from 0 to ℓ

The implication of this is that there will be only two p orbitals in the distant universe, correponding to ℓ = 0 and ℓ = 1, instead of three p orbitals as in the Earth.

• The rule for the spin (ms) number is different than in Earth:

- In Earth: s = +1/2 or -1/2 (two possibilities)

- In the distant universe: ms = -1, 0, - 1

Then in each s or p orbital there will be 3 electrons.

3) Electron configuration in the distant universe

Hence, for the element with atomic number 8, which means that the number of electrons is 8, the configuration is:

• 1s³ (because 3 electrons can populate this orbital)
• 2s³ (because 3 electrons can populate the second s orbital
• 2p² (because the 2 remaining electrons can be placed in the orbitals p: remember that in this distant universe there are two p orbitals, so you can accomodate until 6 electrons in them, 2 × 3 = 6.

Conclusion:

• Maximun number of electrons per orbital: 3
• Electron configuration of the element with atomic number 8:

1s³ 2s³ 2p²