Question

`- 6.2 ^(0.1x) = - 100`
​

Answer 1

`x=25.24`

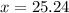
Explanation:

To find the value of
`x`, we are solving the exponential equation
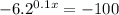`-6.2^(0.1x) =-100` using logarithms.

Let's solve it step-by-step

Step 1. Divide both sides of the equation by -1 to get rid of the negative signs:

`-6.2^(0.1x) =-100`

`(-6.2^(0.1x))/(-1) =(-100)/(-1)`

`6.2^(0.1x) =100`

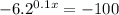
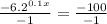
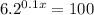
Step 2. Take natural logarithm to bot sides of the equation:

`ln(6.2^(0.1x))=ln(100)`

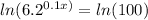
Step 3. Use the power rule for logarithms:
`ln(a^(x) )=xln(a)`

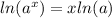
For our equation:
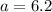`a=6.2` and
`x=0.1x`

`ln(6.2^(0.1x))=ln(100)`

`0.1xln(6.2)=ln(100)`

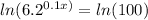
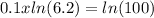
Step 4. Divide both sides of the equation by
`0.1ln(6.2)`

`0.1xln(6.2)=ln(100)`

`(0.1xln(6.2))/(0.1ln(6.2)) =(ln(100))/(0.1ln(6.2))`

`x=(ln(100))/(0.1ln(6.2))`

`x=25.24`

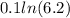
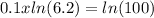
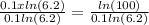
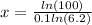
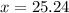
We can conclude that the value of x in our exponential equation is approximately 25.24.