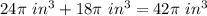Answer:
Part 1)
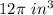
Part 2)

Part 3)
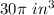
Part 4)
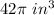
Explanation:
Part 1) Find the volume of the cone
The volume of the cone is equal to
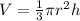
we have
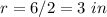 ----> the radius is half the diameter
----> the radius is half the diameter
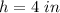
substitute
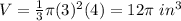
Part 2) Find the volume of a hemisphere (top of the snow cone)
The volume of a hemisphere is
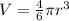
we have
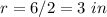 ----> the radius is half the diameter of the base's cone
----> the radius is half the diameter of the base's cone
substitute
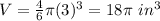
Part 3) How many cubic inches of snow cone will you be serving?
Adds the volume of the cone and the volume of the top
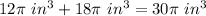
Part 4) Find the volume of the new cone
The volume of the cone is equal to
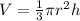
we have
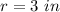
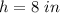
substitute
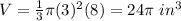
The volume of the top is the same, because the diameter of the cone is the same
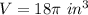
Adds the volume of the new cone and the volume of the top