Answer:
3.1 seconds
Explanation:
The time it will hit the ground is when the height is equal to 0. So we plug in 0 in h and solve the quadratic equation for t.
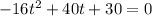
We will use the quadratic formula [
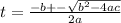 ] to solve this.
] to solve this.
a is -16
b is 40 , and
c is 30.
plugging these into the formula we get:
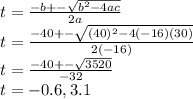
Since time cannot be negative, we take t = 3.1 as the value
So it will take 3.1 seconds to hit the ground (target)