Answer:
The percentage of the students scored higher than 89% is 15.87%.
Explanation:
Given : The average test scores for a particular test in Algebra 2 was 84 with a standard deviation of 5.
To find : What percentage of the students scored higher than 89%?
Solution :
The formula to find z-score is

Where,
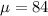 is the mean or average
is the mean or average
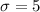 is the standard deviation
is the standard deviation
x=89 is the number
Substitute the value in the formula,
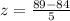
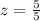
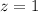
Now, we have to find the percentage of the students scored higher than 89%
From the z-table the value of z at 1 is 0.8413.
Percentage of students scored higher than 89% is
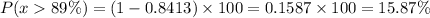
Therefore, The percentage of the students scored higher than 89% is 15.87%.