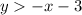Question

What is the slope intercept form?

Answer 1

For this case, we find the equation of the line of the form:

`y = mx + b`

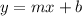
Where:

`m = \frac {y2-y1} {x2-x1} = \frac {-3-0} {0 - (- 3)} = \frac {-3} {3} = - 1`

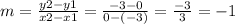
So, we have:

`y = -x + b`

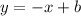
We substitute one of the points:
`0 = - (- 3) + b\\0 = 3 + b\\b = -3`

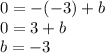
Thus, the equation is:

`y = -x-3`

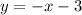
Now, we substitute a point belonging to the region to determine the sign.

(
`(0,0)\\0? - (0) -3\\0? -3`

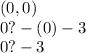
-3 is less than 0.

Then, the inequality is:

`y> -x-3`

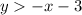
As the border of the region is dotted, then it remains ">."

Answer:

`y> -x-3`