Question

A retail outlet for calculators sells 700 calculators per year. it costs ​$2 to store one calculator for a year. to​ reorder, there is a fixed cost of ​$7​, plus ​$1.65 for each calculator. how many times per year should the store order​ calculators, and in what lot​ size, in order to minimize inventory​ costs?

Answer 1

if Andre orders 500 boxes at a time his anual inventory cost with holding cost included should be $150,030.

Step-by-step explanation:

Answer 2

Times to order: 10 times

Lot size to order: 70 calculators per order

Step-by-step explanation:

Economic Order Quantity is the quantity that minimizes inventory relevant cost-holding cost and ordering cost.

So the number of times to order per year in order to minimize inventory costs can be obtained by using Economic Order Quantity (EOQ) formula:

EOQ=
`√(2OD)/H`

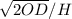
O= ordering cost per order, D = Annual demand and H= holding cost (storage cost)

EOQ =
`√(2*7*700)/2`

EOQ=
`√(9800)/2`

EOQ=
`√(4900)`.

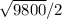
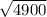EOQ= 70 units.

So the number of times to order per year to minimize inventory cost is given by dividing annual demand by economic order quantity :

Annual demand (D)

= _____________

EOQ

700

= ___

70

= 10 times.