Question

Ella completed the following work to test the equivalence of two express

What conclusion can you draw from Ella’s work?
The expressions are equivalent because Ella got a different result when she substituted zero for f.
The expressions are equivalent because Ella got the same result when she substituted zero for f.
The expressions are not equivalent even though Ella got the same result when she substituted zero for f.
The expressions are not equivalent because Ella did not know that you can’t use substitution to test for equivalence.

Answer 1

Step-by-step explanation: Well it ain't D. I took the test and got it wrong. I am gonna say it's c but if you find other evidence that it's not c go with that. I'm not sure but it's better luck than d.

Answer 2

The expressions are not equivalent because Ella did not know that you can’t use substitution to test for equivalence.

Explanation:

Equivalent algebraic expressions are those expressions which on simplification give the same resulting expression.

Two algebraic expressions are said to be equivalent if their values obtained by substituting any values of the variables are same.

Two expressions 3f+2.6 and 2f+2.6 are not equivalent, because when f=1,

`3f+2.6=3\cdot 1+2.6=3+2.6=5.6\\ \\2f+2.6=2\cdot 1+2.6=2+2.6=4.6\\ \\5.6\\eq 4.6`

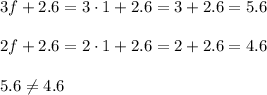
Method of substitution can only help her to decide the expresssions are not equivalent, but if she wants to prove the expressions are equivalent, she must prove it for all values of f.

`3f+2.6=2f+2.6\\ \\3f=2f\\ \\3f-2f=0\\ \\f=0`

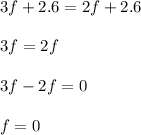
This is true only when f=0.

Hence,

The expressions are not equivalent because Ella did not know that you can’t use substitution to test for equivalence.