Question

You have 2 different savings accounts. For Account​ A, the simple interest earned after 9 months is ​$5.70. For Account​ B, the simple interest earned after 27 months is ​$32.40. If the interest rate is 3.8​% for Account A and 2.4​% for Account​ B, how much is the principal in each​ account? Which account earned you the most interest the first​ month? Explain your answer.

Answer 1

Principal in account A = $200

Principal in account B = $600

Account B earned more interest in the first month.

Explanation:

Given two accounts:

Account A:

Time = 9 months =
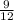`(9)/(12)` years

Interest rate = 3.8%

Interest earned = $5.70

Account B:

Time = 27 months =
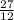`(27)/(12)` years

Interest rate = 2.4%

Interest earned = $32.40

To find:

Principal in each account.

Most interest earned in the first month?

Solution:

First of all, let us have a look at the formula for Simple Interest.

`SI = (P* R* T)/(100)`

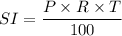
Putting the values for Account A and finding the value of Principal:

`5.70 = (P_A * 3.8* 9)/(100* 12)\\\Rightarrow P_A = (570* 12)/(3.8* 9)\\\Rightarrow P_A=\$200`

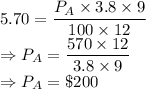
Now, Putting the values for Account B and finding the value of Principal:

`32.40 = (P_B * 2.4* 27)/(100* 12)\\\Rightarrow P_B = (3240* 12)/(2.4* 27)\\\Rightarrow P_B=\$600`

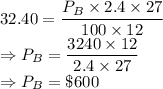
Interest earned in one month i.e.
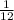`(1)/(12)` years:

Account A:

`SI_A = (200* 3.8* 1)/(100* 12)\\\Rightarrow SI_A = \$0.63`

`SI_B = (600* 2.4* 1)/(100* 12)\\\Rightarrow SI_B = \$1.2`

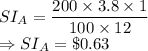
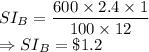
Account B earned more interest in the first month.

Therefore, the answers are:

Principal in account A = $200

Principal in account B = $600

Account B earned more interest in the first month.