Answer:
The graph in the attached figure
Explanation:
we have

Find the intercepts
The y-intercept is the value of y when the value of x is equal to zero
so
For x=0 ----->
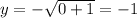
The y-intercept is the point (0,-1)
The x-intercept is the value of x when the value of y is equal to zero
so
For y=0 ----->
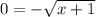 ----->
----->

The x-intercept is the point (-1,0)
Find the domain
we know that
The radicand must be positive
so
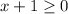

All real numbers greater than or equal to -1
The range is all real numbers less than or equal to -1
using a graphing tool
see the attached figure