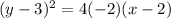Question

A parabola has its focus at (0, 3) and its directrix at x = 4. What is the focal length of the parabola? Explain how you determined this. What is the equation, in standard form, of the parabola? Explain how you determined this.

Answer 1

p=2

Standard form;
`(y-3)^2=4(-2)(x-2)`

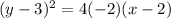
Explanation:

The focal length of the parabola is the distance from the vertex to the focus of the parabola.

The focus of the parabola is (0,3).

The equation of the directrix is x=4

The distance from the focus to the direction is |4-0|=4

Half of this distance is the same as the distance from the focus to the vertex.

Therefore the focal length is
`(4)/(2)=2`

The vertex of the parabola is (2,3)

The standard form of the parabola is

`(y-k)^2=4p(x-h)`

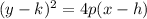
The parabola is opens along the negative x-axis

`(y-3)^2=4(-2)(x-2)`

`(y-3)^2=-8(x-2)`