Answer:
y-intercept at (0, 3)
horizontal asymptote of y = 0
no x-intercept
Explanation:
Definitions
y-intercept: the point(s) at which the curve crosses the y-axis (when x=0).
x-intercept: the point(s) at which the curve crosses the x-axis (when y=0).
Asymptote: a line that the curve gets infinitely close to, but never touches.
Given function:
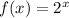
Properties of function f(x):
- y-intercept at (0, 1)
- As x → -∞, y → 0 therefore there is a horizontal asymptote at y=0 and no x-intercept (since the curve never crosses the x-axis).
- As x → ∞, y → ∞
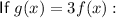
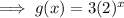
Properties of function g(x):
- y-intercept at (0, 3)
- As x → -∞, y → 0 therefore there is a horizontal asymptote at y=0 and no x-intercept (since the curve never crosses the x-axis).
- As x → ∞, y → ∞
Therefore the true statements are:
- y-intercept at (0, 3)
- horizontal asymptote of y = 0
- no x-intercept