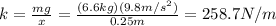Question

A block with mass m =6.6 kg is hung from a vertical spring. When the mass hangs in equilibrium, the spring stretches x = 0.25 m. While at this equilibrium position, the mass is then given an initial push downward at v = 4.3 m/s. The block oscillates on the spring without friction. 1) What is the spring constant of the spring?

Answer 1

258.7 N/m

Step-by-step explanation:

The spring constant can be found by considering the equilibrium position only. In fact, in that situation, we have that the mass of m = 6.6 kg hangs on the spring, stretching it by x = 0.25 m.

The weight of the block of mass m is equal in magnitude to the restoring force of the spring, given by Hooke's law:

`F=mg=kx`

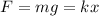
So, from this equation, we can find the spring constant of the spring:

`k=(mg)/(x)=((6.6 kg)(9.8 m/s^2))/(0.25 m)=258.7 N/m`