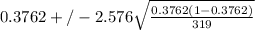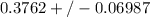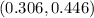Question

When 319 college students are randomly selected and surveyed , it is found that 120 own a car . Find a 99% confidence interval for the true proportion of all college students who own a car.

A.0.306

B.0.323

C.0.313

D.0.332<0.421

Answer 1

`(0.306,0.446)`

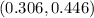
Explanation:

The confidence interval for a population proportion is calculated using the formula;

`p+/-z\sqrt{(p(1-p))/(n) }`

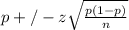
In the above expression;

p represents the sample proportion calculated as, number of successes/sample size;

p = 120/319 = 0.3762

z represents the confidence coefficient associated with the given level of significance. In our case the confidence level required is 99%. The z-score associated with this level of significance is +/-2.576

n represents the sample size under evaluation, 319 college students.

Using the values obtained above, the 99% confidence interval for the true proportion of all college students who own a car is;

`0.3762+/-2.576\sqrt{(0.3762(1-0.3762))/(319) }`

`0.3762+/-0.06987`

`(0.306,0.446)`